人工智能（AI）指的是像人类一样思考和行为的一种仿真计算机程序。人工智能也可以指表现出与人的思维有关的特征（例如学习和解决问题）的任何机器或计算机系统。与传统的自动地震数据分析算法不同，传统的方法是基于地震学理论来分析新数据，而人工智能方法是利用大量的历史地震和经验来分析判断新的地震信息，智能地动系统将传统理论方法与人工智能方法结合起来处理新的地震事件，因此结果更准确。

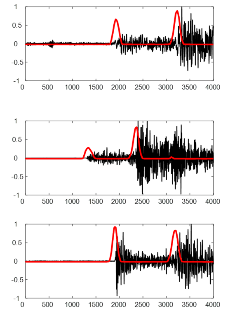
检测、发现地震事件是地震监测的第一步。通常大中型地震由于其信噪比高而很容易检测出来；我们主要关注的是具有挑战性的小地震的事件检测问题。由于庞大的地震数据量，依靠人工检测地震事件是非常困难的。

在过去几十年中开发的多种检测方法中，最流行的一种是长短时窗比较算法（STA / LTA）（Allen, 1978）。模板匹配方法算法稳定，但是需要在事件检测之前选择模板（Gibbons＆ Ringdal, 2006; Shelly et al., 2007）。这些都是单分量的地震检测方法；如果噪声不明显，则效果较好。

微小地震事件通常在振幅上是很模糊的，但是有些一致的模式。因此，很自然地联想到应用机器学习来帮助检测地震事件。到目前为止，已经发表了许多应用机器学习进行事件检测的方法的论文。这些方法包括单台站法和多台站法（Perol et al.，2018; Wu et al.，2018; Chen，2018; Zhu＆Beroza，2018; Ross et al.，2018; Mousavi et al.，2018; Chen et al.，2019; Dokht et al.，2019; Zhou et al.，2019; Pardo et al.，2019; Wang et al.，2019; Zhu et al.，2019）。所有这些方法检测到的地震事件数目远远超过地震目录中列出的地震事件的数目。这些研究结果表明人工智能技术在地震检测方面已经超越了人工检测能力，已经毫无悬念。智能地动系统采用FCN方法来检测事件，并将深度学习与常规方法相结合来确保结果的可靠性。

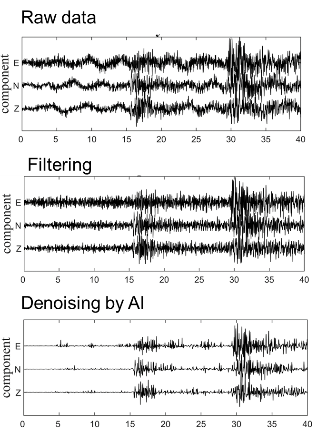
地球上发生着很多微小地震，它们携带着来自地球内部的很多重要信息。然而，较小的地震信号更易于受噪声影响，因而很难被检测到。频率域滤波是抑制噪声的最常用的方法，但是当噪声和地震信号在同一频率范围时，这种方法就出现了局限性。此外，各个地震数据不同，最佳滤波参数的选择也比较困难，错误地选择滤波参数很可能会改变波形数据，导致后续分析结果不正确。

目前在数据处理中，比较前沿的去噪方法主要是基于不同域的变换。其中包括短时傅里叶变换(STFT) (Mousavi & Langston, 2016)、小波变换(Cao & Chen, 2005; Gaci, 2014; Liu et al.，2016) 和曲波变换(Hennenfent & Herrmann, 2006; Neelamani et al.，2008; Tang & Ma, 2008)等方法。然而，地震噪声是随时间和地点的变化而变化的，所以需要能处理各种情况的更有效的解决办法。

采用人工智能DnCNN的图像去噪方法是能有效解决问题的方案之一，该方法最初被提出用于处理图形图像(Zhang et al., 2017)。该方法是一种深度学习中的残差学习网络，可用于多站地震数据的时域去噪。深度学习是一种强大的机器学习技术，可以通过神经网络学习极其复杂的函数。DnCNN方法不需要估计噪声水平，可自适应降噪，而且它不受信号和噪声频率范围的限制。为了获得小地震所需的训练样本，我们用Richter公式对中、大地震信号降震级处理。将该方法应用于川滇地区取得了令人满意的结果(Wang & Zhang, 2019)。

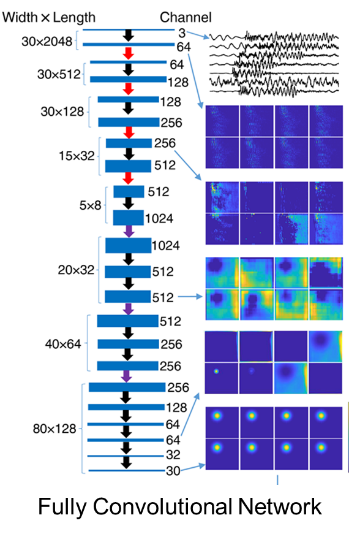
快速准确地定位地震是地震监测中的一项重要任务，它将有助于监测和研究地震活跃的断层、俯冲带，并给当地地区提供潜在危险性的评估。传统的地震定位方法包括走时反演（Thurber, 1985; Lienert et al., 1986），网格搜索（Sambridge & Kennett, 1986; Nelson & Vidale, 1990）和双差定位（Waldhauser & Ellsworth, 2000）等。这些基于走时拾取的方法虽然只针对较大的地震事件表现出较高可信度，但是它们非常的稳定和高效。地震波形匹配方法相对于基于走时拾取的方法应该可以得到更准确的地震位置解（Kao & Shan, 2004; Grigoli et al., 2014），但会大大增加计算时间和工作量。

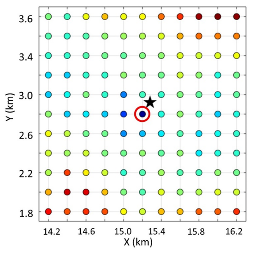
无论是多大的地震事件，我们的目标是当它们发生后立即对它们进行定位。小地震的位置信息能够充分说明地下的地震活动性，但由于小震信号的信噪比低，因而很难定位。幸运的是，人工智能图像识别技术在定位小震和大震方面的应用被证明是稳定的（Wang & Zhang, 2019; Zhang et al., 2020）。人工智能方法需要大量的记录数据来训练神经网络系统，不需要依赖任何速度模型，它在具有活跃地震活动和大量历史地震事件记录的区域是可应用的。随着多台站三分量数据的输入，神经网络的输出是对应地球上地震位置概率的三维数据体，这一过程只需要不到一秒钟的处理时间。

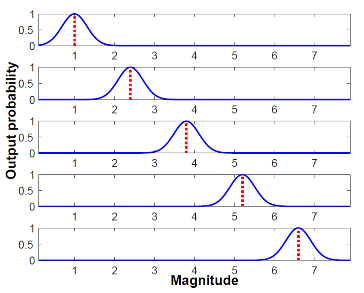
地震震级对公众至关重要，因为震级的大小影响着我们的生活。根据使用波形信息的不同和方法的不同，有三种震级标定：里氏震级（ML）、面波震级（Ms）和矩震级（Mw）(Richter, 1935; Gutenberg, 1945a; Gutenberg, 1945b; Havskov & Ottemöller, 2010)。其中，里氏震级被更广泛地用于中小地震。通常在计算里氏震级时，我们首先计算每个地震台站记录的地震波幅值，然后通过取平均值得出地震事件的最终里氏震级（Havskov＆Ottemöller，2010）。由于地震源的辐射花样和每个地震台站的场地效应的不同，不同的台站上测得地震波振幅有很大的差异，会导致震级估计值不一致（Aki，1993）。

解决此问题的有效解决方案之一是应用机器学习来预测地震震级（Reddy＆Nair，2013）。应用机器学习的一个重要条件是准备足够的训练数据集，大型训练数据集应更好地尽可能平均地分配给每个输出标签，以解决过度拟合的问题（Jaitly＆Hinton，2013）。但是，在实际情况下，根据地震强度和地震频度的关系（Gutenberg＆Richter，1954），小地震自然要比大地震多得多。为了减轻这一困难，我们根据里氏幅度公式通过幅度缩放从实际数据中创建了足够的训练数据集。准备好训练数据后，我们设计了一个FCN网络来估计地震震级。

我们提出了地震搜索引擎的想法，并在2014年和2016年发表了相关文章（Zhang et al.，2014; Zhang＆Zhang, 2016）。这种方法需要建立包含合成数据或真实数据的大型数据库。搜索引擎将搜索出与输入地震最匹配的地震图。从最匹配的地震图包含的地震震源信息，我们可以得出输入地震的震源信息。这个想法类似于计算机图像搜索引擎。

从大型数据集中搜索相似图像是经典的计算机问题之一。在计算机搜索领域中，数据中的采样点数被视为其“维度”。地震图相似性搜索是一个高维问题，需要很大的计算量才能从庞大的数据库中搜索真实的解。在保留有效信息的前提下，降维方法用少量的数据采样点代替时间域上大量的采样点（Jolliffe，1986）。除了降维，我们采用近似近邻搜索方法，该方法可以比精确搜索快几个数量级，同时仍提供接近最佳的精度（Muja＆Lowe，2009）。

现有的快速搜索方法是基于哈希结构或基于树状结构的，例如局部敏感哈希（LSH）（Slaney＆Casey，2008）和多重随机K维（MRKD）树方法（Silpa-Anan＆Hartley，2008; Wu et al.，2011）。在比较了两类搜索地震图的方法之后，我们发现对于各种大小的高维地震图数据集，MRKD树方法始终是更快的。 Silpa-Anan和Hartley（2008）以及Muja和Lowe（2009）也指出，MRKD树方法在处理高维数据的计算机视觉问题中有明显得优势。此方法在差异最大的采样点处划分数据，建立多个树形结构。该数据集在有限的样本中捕获了地震数据中最突出的特征。然后，当我们输入地震时，将按照树结构搜索最佳匹配。该方法需要进行log2N次比较，以从一棵树中找到最佳匹配的第一个候选对象，其中N是数据库中地震图的数量（Friedman et al.，1977）。如果需要更多的搜索结果，则需要额外的沿树形结构计算。

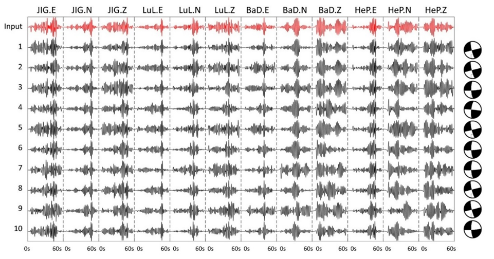
类似于图像搜索引擎，我们提出了地震搜索引擎系统，这是一个可以搜索出与输入地震相似的地震的系统。该系统分析大量的已知震源参数的实际地震波形和理论地震波形。通过应用计算机快速搜索算法，创建的结构化数据库能够使搜索结果在一秒内得出。地震搜索引擎的输入是来自多个台站的三分量地震记成的一个“图形化图像”。输出的结果是一系列按照相似度显示的相似图像。每幅图像都代表了一个带有详细震源参数的解。因此，最佳匹配的图像表示最优解。

压缩感知突破了传统的数据采集的方法，该领域的先驱者包括D. Donoho，E. Candès，和T. Tao。许多自然信号有着简洁的表达法而且有着充足的随机采样点，压缩感知就是利用其稀疏或可压缩的性质。该方法可以用于预测以前没有发生地震地区的地震图。

传统采样信号或图像的方法遵循著名的香农定理:采样率必须至少是信号中存在的最大频率的两倍（即奈奎斯特频率）（Candès & Wakin, 2008）；否则，将出现混叠。然而，压缩感知理论认为，与传统方法相比，人们可以从更少的样本或测量中恢复特定的信号和图像（Candès & Tao, 2006; Donoho, 2006; Baraniuk, 2011）。

在医学成像中应用压缩感知时，生成相同分辨率的图像可能需要的数据要少得多。例如，压缩感知在X射线计算机断层扫描（CT）中的应用，使用欠采样因子32的数据来精确重建动态CT图像，可以得到与全部数据成像几乎相同的解析度，但在CT成像中将辐射剂量减少了32倍（Chen et al.，2008）。

与医学成像类似，勘探地震数据采集也应受益于这种方法。然而，相较于医学成像，地震数据采集工程昂贵、复杂，因此地震数据采集更加地保守，不希望出现数据不足、重新采集的情况。当前，在油气勘探地震数据采集中，对于相同数量的数据，采用CS技术可以减少50%以上的震源数量和作业时间(Mosher et al., 2014)，节省了大量的成本。

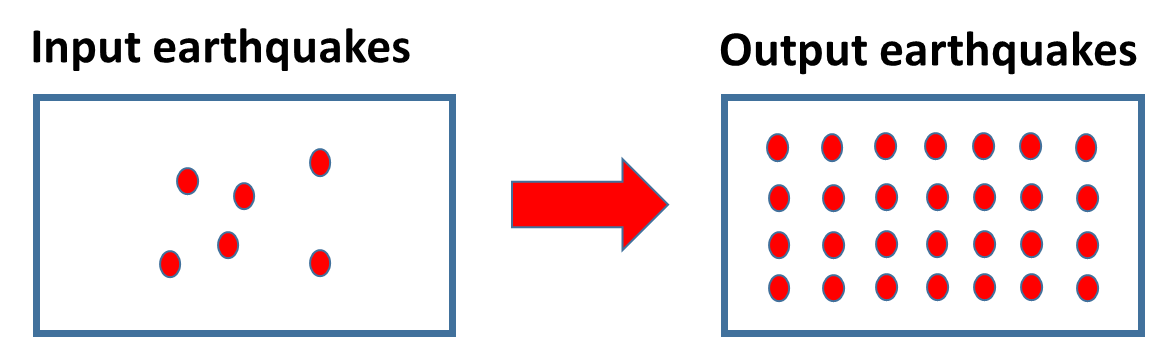
当前的地震学理论提供了多种应用模型来模拟计算人工合成地震数据。基于地球结构（或模型）的假设，通过求解弹性波动方程可以计算出合成的地震记录。尽管人们一直在努力利用前沿的成像技术来探索地球内部的三维各向异性结构（Wang et al.，2008；Tape et al.，2009），但用于正演模拟的地球模型仅仅只代表我们对地球目前的最佳了解，不一定是准确的地下结构。由于地震的分布以及地震台站的覆盖范围有限，当前的地震学方法还不能使用对地震或台站插值计算，获取任意位置的地震图。但是新的压缩感知理论方法可以帮助我们从稀疏分布的地震事件数据中重建出任意一点的新的地震数据，并用于地震定位快速搜索的数据库。